ত্রিকোণমিতির সূত্র অনুপাতগুলো মনে রাখার টেকনিক PDF
ত্রিকোণমিতির সূত্র PDF
ত্রিকোণমিতির সূত্র PDF: ত্রিকোণমিতির সূত্র ও অনুপাতগুলো গুলো মনে রাখতে পারলে আপনারা অতি সহজেই যে কোন ত্রিকোণমিতির সমস্যা সমাধান করতে পারবেন। চলুন আগে দেখে নেই ত্রিকোণমিতির অনুপাতগুলো মনে রাখার টেকনিক ও সহজ পদ্ধতি
ত্রিকোণমিতি কাকে বলে?
ত্রিকোণমিতি গণিতের একটি শাখা, যাতে ত্রিভুজের কোণ, বাহু ও তাদের মধ্যকার সম্পর্ক ব্যবহার করে বিভিন্ন সমস্যার সমাধান করা হয়, তাকে ত্রিকোণমিতি (Trigonometry) বলে। ত্রিকোণমিতির দুটি শাখার একটি সমতলীয় ত্রিকোণমিতি এবং অপরটি গোলকীয় ত্রিকোণমিতি।
বিশেষ করে ত্রিভুজের তিনটি কোণের অপেক্ষকগুলো নানা পরিমাপের কাজে লাগানো যায়। ত্রিভুজের একটি কোণের ছয়টি অপেক্ষক বা ফাংশন থাকে যথা সাইন (sine), কোসাইন(cosine), ট্যানজেন্ট(tangent), কোট্যান্জেন্ট(cotangent), সেক্যান্ট(secant) এবং কোসেক্যান্ট(cosecant)। এগুলো ব্যবহার করে অজানা কোণ ও দূরত্ব পরিমাপ করা হয়।
ত্রিকোণমিতি শব্দের অর্থ কী?
ইংরেজি “Trigonometry” শব্দটি গ্রিক শব্দ “trigōnon” বা “ত্রিভুজ” এবং “metron” বা “পরিমাপ” থেকে উদ্ভূত হয়েছে।
ত্রিকোণমিতির ইতিহাস
এটি গণিতের প্রাচীনতম শাখাগুলোর একটি হল ত্রিকোণমিতি। ত্রিকোণমিতির জন্ম প্রাচীন মিশরে হলেও এর আদি উদ্ভাবক একজন গ্রিক জ্যোতির্বিদ যার নাম হিপারকাস। খ্রিষ্টপূর্ব দ্বিতীয় শতকে গ্রিক হিপারকাস গ্রহ-নক্ষত্র ও তাদের মধ্যবর্তী বেগ এবং দুরত্ব নির্ণয় ও বিচার করতে গিয়ে এই বিদ্যার চর্চা শুরু করেন। তিনি কাজ করতেন আলেকজান্দ্রিয়ার একটি জাদুঘরে। তবে আমরা বর্তমান যুগে ‘থেটা’, ‘সাইন’, ‘কস’, ‘কোসাইন’, ‘কোসেক’ ইত্যাদি দিয়ে যে ত্রিকোণমিতি করে থাকি তার উদ্ভাবক মুসলিম গণিতবিদেরা। নবম খ্রিষ্টাব্দে আবু আবদুল্লাহ আল-বাতানি, হাবাস আল-হাসিব ও আবুল ওয়াফা আল-বুজানি নামের তিন গণিতবিদের যৌথ উদ্যোগের ফসল আধুনিক ত্রিকোণমিতি। তবে তারা গ্রিক জ্যোতির্বিদ হিপারকাসের মূল ধারণার ওপর ভিত্তি করেই এ বিষয়টিকে আরও আধুনিক করে গড়ে তুলেছিলেন।
সূর্যের গতি ও সময় নির্ণয়ের প্রাচীনতম যন্ত্র “Shadow Stick”-এ প্রথম ব্যবহৃত হয়েছিল এই ত্রিকোণমিতি। এছাড়া পরবর্তীতে ত্রিকোণমিতি ব্যবহার করে অনেক ধরনের ঘড়ি আবিষ্কৃত হয় যেগুলো বিভিন্ন নক্ষত্রের সাহায্যে সময় নির্ণয় করতে পারত। যেমন- Gonon Circle, Merkhet ইত্যাদি। অক্ষাংশ ও দ্রাঘিমাংশ নির্ণয়েও ত্রিকোণমিতি ব্যবহৃত হয়। ত্রিকোণমিতির ধারণাকে কাজে লাগিয়ে প্রাচীন জ্যোতির্বিদরা ঋতু নির্ণয় করেছিলেন যা সেই সময় বড় বড় প্রাকৃতিক দুর্যোগ যেমন- বন্যা, খরা, ঘূর্ণিঝড় ইত্যাদির পূর্বাভাস দিতে সাহায্য করেছিল।
আরও পড়ো-
- সহস্র শর্টকাট পদ্ধতি গাণিতিক সূত্র সহ বাংলায় লেখা বই PDF Free
- ক্যালেন্ডার অঙ্ক শর্টকাট সূত্র
- ঘড়ির কাঁটার মধ্যবর্তী কোণ নির্ণয় করার শর্টকাট পদ্ধতি
- অনুপাত ও সমানুপাত
- কাজ ও সময় সম্পর্কিত অংকের শর্টকাট সূত্র
- ত্রিকোণমিতির অনুপাতগুলো মনে রাখার টেকনিক
- নৌকা ও স্রোত সংক্রান্ত অংক করার শর্টকাট টেকনিক
- লাভ ক্ষতির অংক করার শর্টকাট টেকনিক
ত্রিকোণমিতির অনুপাতগুলো মনে রাখার টেকনিক ও সহজ পদ্ধতি
শর্টকাট টেকনিক – ১
Sin,Cos,Tan ত্রিকোণমিতির সূত্র অনুপাত গুলো মনে রাখার সহজ উপায়ঃ
# ফর্মূলাঃ
ল’তি…ভূ’তি…লভূ
ল’তি=লম্ব ÷ অতিভুজ=Sin
ভূ’তি=ভূমি ÷ অতিভূজ=Cos
লভু=লম্ব ÷ ভূমি=tan
সতর্কতাঃ
Sin এর বিপরীত cosec
cos এর বিপরীত Sec
tan এর বিপরীত cot
শর্টকাট টেকনিক – ২
ত্রিকোনমিতির সূত্র মনে রাখার সহজ উপায়ঃ
সাগরে লবণ অনেক
=>SIN= লম্ব ÷ অতিভুজ
কবরে ভূত অনেক,
=>COS= ভূমি ÷ অতিভুজ
ট্যারা লম্বা ভূত।
=>TAN= লম্ব ÷ ভূমি।
[আরও পড়ুন- নৌকা ও স্রোত সংক্রান্ত অংক করার শর্টকাট টেকনিক]
ত্রিকোণমিতির অনুপাতগুলো মনে রাখার টেকনিক ও সহজ পদ্ধতি
আমাদের জীবনে সমকোণী ত্রিভুজের ব্যবহার অনেক। আমাদের পরিবেশে কল্পনায় হাজারো সমকোণী ত্রিভুজ গঠন করা যেতে পারে। এই সমকোণী ত্রিভুজ ব্যবহার করে, আমরা গাছে না উঠেও সহজে বের করতে পারি গাছের উচ্চতা, বের করতে পারি নদীর প্রস্থ থেকে শুরু করে দূরবর্তী গ্রহ নক্ষত্রের দূরত্ব। আর এই গাণিতিক কৌশলের ভিত্তিতেই সৃষ্টি হয়েছিল ত্রিকোনমিতি নামক গণিতের বিশেষ শাখা। এটি মূলত ৩ কোণের পরিমাপের বিষয় নিয়েই সৃষ্টি।
আমরা সকলেই জানি যে, যেকোন কোণের (সমকোণ ব্যাতিত) ছয়টি ত্রিকোণমিতিক অনুপাত পাওয়া যায়। যথাঃ sin@,cos@,tan@,cosec@,sec@ ও cot@.
আমরা পাঠ্যাবইয়ের বিভিন্ন সমস্যার সমাধান করবার জন্য সাধারনত (০,৩০,৪৫,৬০,৯০) এই ৫ টি কোণের জন্য বাহুদ্বয়ের অনুপাত বের করি এবং এগুলো দিয়েই বিভিন্ন বাস্তবিক সমস্যার সমাধান করি। তবে সমস্যা হলো ৬ টি ত্রিকোনমিতিক অনুপাতের ৫ টি কোণের জন্য অনুপাতসমূহ(৩০ টি) মুখস্থ করতে অনেকেরই সমস্যা হয়। অনেক ছাত্রছাত্রী তো মুখস্থ না করেই ক্যালকুলেটর বা বইয়ের সাহায্য নিয়ে পড়াশোনা শেষ করে দিতে চাই। অনেকেই আবার মুখস্থ করেও ভুলে যায়। অনেকের ভালোভাবে মুখস্থ থাকলেও পরীক্ষার সময়ে সন্দেহ সৃষ্টি হয় বা গুলিয়ে দিয়ে ভুল করে দেয়।
তাই খুব সহজেই ত্রিকোণমিতিক এই অনুপাতগুলো মনে রাখার কৌশল খুবই জরুরী।
চলুন এবার তবে সেই কৌশল শিখা যাক যে কি করে সহজেই খুবই অল্প সময়ে এই অনুপাতগুলো বের করা যায়।
[আরও পড়ুন- গণিতের সকল সূত্রের শর্টকাট জানুন। অসংখ্য টিপস একসাথে জানুন]
আপনারা সকলেই নিশ্চয়ই চিত্রে একটি হাতের ছবি দেখতে পাচ্ছেন।
এবার হাত এর ছবিতে লক্ষ্য করেছেন নিশ্চয়ই যে ৫ টি আঙুলকে (০,৩০,৪৫,৬০,৯০) কোণের চিহ্ন হিসেবে ধরা হয়েছে। এবার চলুন নিজ নিজ হাত দিয়ে অনুপাতগুলো বের করি।
প্রথমে sin এর ৫টি কোণের অনুপাত বের করি চলুন।
নিজ নিজ হাতের আঙুলগুলোকে চিত্রের হাতের মতো করে ভাবুন। এই sin এর অনুপাতগুলো বের করার জন্য যে কোণের মান বের করবেন সেই কোণ অনুযায়ী চিত্রের ছবির মতো আঙুল সিলেক্ট করুন। তারপর দেখুন যে ঐ আঙুলের বাম পাশে কতটি আঙুল আছে। বামপাশে যতগুলে আঙুল থাকবে, তার বর্গমূল করে ২ দিয়ে ভাগ করলেই, ঐ কোণের মান পেয়ে যাব আমরা।
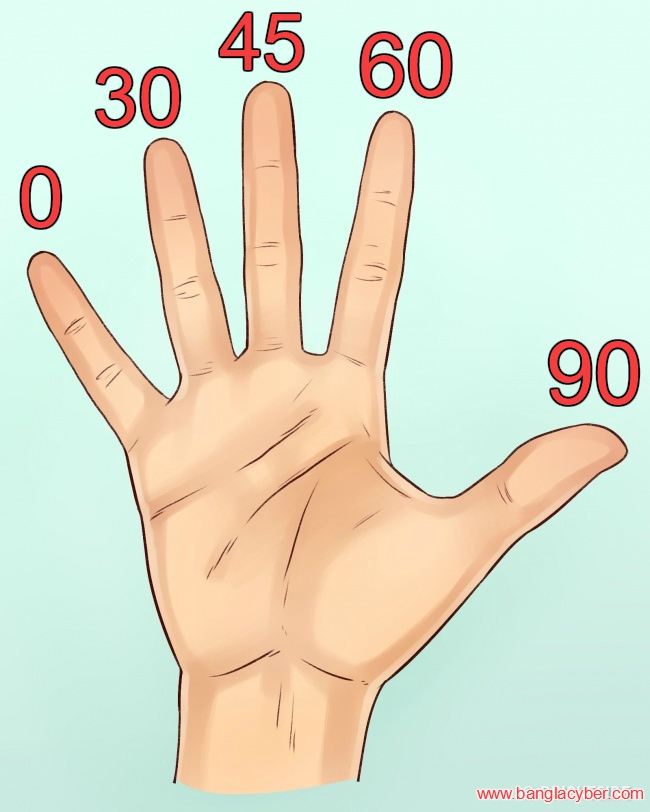
উদাহরণঃ এবার sin0 ডিগ্রী এর মানের জন্য আমরা ভাবি। চিত্রের হাতের ০ লেখা জায়গার বামপাশে কি আর কোন আঙুল আছে..?
না,নেই। (সুতরাং, ০ টি আঙুল আছে)
তার মানে ০ কে বর্গমূল করে ২ দিয়ে ভাগ করলেই sin0 এর মান পাওয়া যাবে।
সুতরাং,sin0= √ 0/2 =0
অনুরুপভাবে,sin30= √ 1/2 =1/2
sin45= √ 2/2 = √2/ √2* √2 =1/ √2
sin60 = √3/2
sin90= √4/2=2/2=1
sin এর অনুপাতগুলো পেয়ে যাবার মানে cosec এর অনুপাতগুলোও পেয়ে গেছি।
কারন, sin@=1/cosec@
তাই,cosec0=1/0=অনির্ণেয়
cosec30=2….(এভাবে বের করতে হবে)
আমরা sin এর অনুপাতগুলো বের করতে শিখলাম। এবার আমরা cos এর অনুপাতগুলো বের করতে শিখব।
cos এর কোণের অনুপাতসমূহ বের করার পদ্ধতি sin এর মতোই,শুধুমাত্র একটু উল্টা।
cos এর ক্ষেত্রেও আমার ছবির মতো আঙুল সিলেক্ট করতে হবে। এরপর যে কোণের মান বের করব সেই কেণ সিলেক্ট করা আঙুলের ডানপাশের আঙুল সংখ্যা হিসেব করে বর্গমূল করার পরে ২ দিয়ে ভাগ করলেই,উক্ত কোণের মান পাওয়া যাবে।
উদাহরণঃ এবার cos0 ডিগ্রী এর মানের জন্য আমরা ভাবি। চিত্রের হাতের ০ লেখা জায়গার ডানপাশে কি আর কোন আঙুল আছে..?
৪ টি আঙুল আছে
তার মানে ৪ কে বর্গমূল করে ২ দিয়ে ভাগ করলেই cos0 এর মান পাওয়া যাবে।
cos0= √4/2 =2/2 =1
cos30= √3/2
cos45 = √2/2= √2/ √2. √2=1/ √2
cos60 = √1/2 =1/2
cos90=0/2 =0
এবার cos থেকে আমরা সহজেই sec এর কোণের অনুপাতগুলো বের করতে পারি।
কারণ,cos@=1/sec@
অর্থ্যাৎ,sec=1
sec30=2/ √3(এভাবেই চলবে)
এখন আমরা sin ও cos এর মান থেকে tan এর কোণের অনুপাতগুলো বের করব।
আমরা জানি,tan@=sin@/cos@
সুতরাং,tan0=sin0/cos0
…………….. =0/1=0
tan30=sin30/cos30 =(1/2)/( √3/2) =1/ √3
(এভাবে সহজেই tan এর অনুপাতগুলো বের করলাম)
এরপর cot@ =1/tan@ ব্যবহার করে সহজেই cot এর কোণের অনুপাতগুলোও বের করা যায়।
দেখলেন তো কত্ত সহজেই নিজ নিজ হাত ব্যবহার করেই ত্রিকোণমিতিক
অনুপাতগুলো বের করা সম্ভব।
এখন তো আর ত্রিকোনমিতিক অনুপাতগুলো মুখস্থ করার দরকার নাই।
গণিত এমনই এক জিনিস যাকে বাস্তবতার সাথে কল্পনা করতে পারলে খুব সহজেই সমস্যার সমাধান করা যায়।তাই নিজের চিন্তা-চেতনাকে অবশ্যই বৃদ্ধি করুন।
ত্রিকোণমিতি অধ্যায়ের সূত্রসমূহ
১। cosec θ = 1/sin θ
২। sec θ = 1/cos θ
৩। cot θ = 1/tan θ
৪। sin θ = 1/cosec θ
৫। cos θ = 1/sec θ
৬। tan θ = 1/cot θ
৭। sinθ=1/cosecθ
৮। cosecθ=1/sinθ
৯। cosθ=1/secθ
১০। secθ=1/cosθ
১১। tanθ=1/cotθ
১২। cotθ=1/tanθ
১৩। sin²θ + cos²θ= 1
১৪। sin²θ = 1 – cos²θ
১৫। cos²θ = 1- sin²θ
১৬। sec²θ – tan²θ = 1
১৭। sec²θ = 1+ tan²θ
১৮। tan²θ = sec²θ – 1
১৯। cosec²θ – cot²θ = 1
২০। cosec²θ = cot²θ + 1
২১। cot²θ = cosec²θ – 1
২২। sin (A + B) = sin A cos B + cos A sin B
২৩। sin (A − B) = sin A cos B – cos A sin B
২৪। cos (A + B) = cos A cos B – sin A sin B
২৫। cos (A – B) = cos A cos B + sin A sin B
২৬। tan(A+B) = [(tan A + tan B)/(1 – tan A tan B)]
২৭। tan(A-B) = [(tan A – tan B)/(1 + tan A tan B)]
২৮। sin2A = 2sinA . cosA
= [2tan A/(1+tan2 A)]
২৯। cos2A = cos2A–sin2A
= [(1-tan2 A) / (1+tan2 A)]
৩০। cos2A = 2cos2A−1
= 1–2sin2A
৩১। tan(2x) = [2tan(x)]/ [1−tan2(x)]
৩২। sec (2x) = sec2 x/(2-sec2 x)
৩৩। cos (2x) = (sec x. cos x)/2
৩৪। Sin 3x = 3sin x – 4sin3x
৩৫। Cos 3x = 4cos3x-3cos x
৩৬। Tan 3x = [3tanx-tan3x]/[1-3tan2x]
৩৭। sin x sin y = 1/2 [cos(x–y) − cos(x+y)]
৩৮। cos x cos y = 1/2[cos(x–y) + cos(x+y)]
৩৯। sin x cos y = 1/2[sin(x+y) + sin(x−y)]
৪০। cos x sin y = 1/2[sin(x+y) – sin(x−y)]
৪১। sin C + sin D = 2 sin [(C+D)/2] cos [(C-D)/2]
৪২। sin C – sin D = 2 cos [(C+D)/2] sin [(C-D)/2]
৪৩। cos C + cos D = 2 cos [(C+D)/2] cos [(C-D)/2]
ত্রিকোণমিতিক অনুপাত
- sinθ=लম্ব/অতিভূজ
- cosθ=ভূমি/অতিভূজ
- tanθ=लম্ব/ভূমি
- cotθ=ভূমি/লম্ব
- secθ=অতিভূজ/ভূমি
- cosecθ=অতিভূজ/লম্ব
ত্রিকোণমিতিক কোণের মানঃ
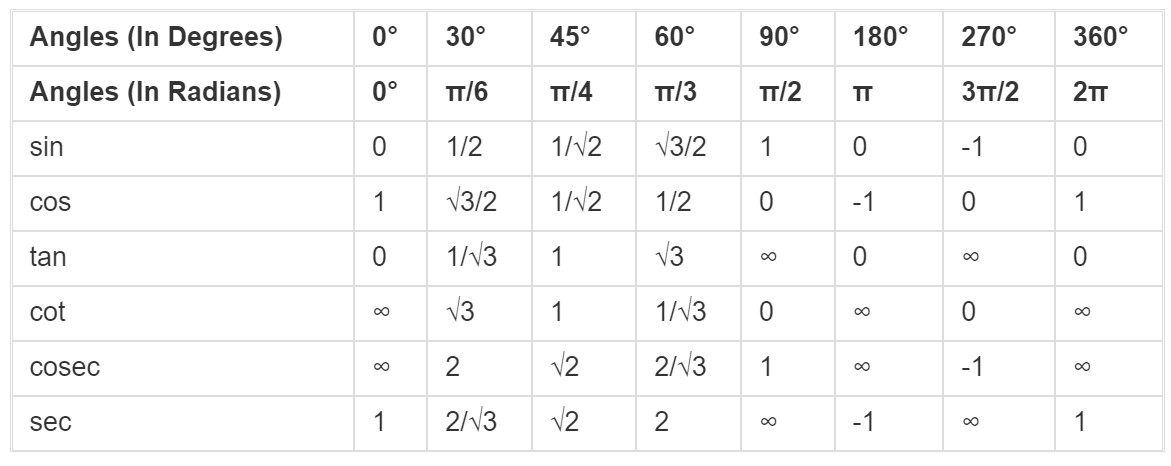
ত্রিভুজ সম্পর্কিত অভেদ
সাইন সূত্র
সাইন সূত্র অনুসারে যে কোনো ত্রিভুজে:
- {\displaystyle {\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R={\frac {abc}{2\Delta }}}
যেখানে {\displaystyle \Delta } হচ্ছে ত্রিভুজটির ক্ষেত্রফল এবং R হল ত্রিভুজটির পরিবৃত্তের ব্যাসার্ধ।
- {\displaystyle R={\frac {abc}{\sqrt {(a+b+c)(a-b+c)(a+b-c)(b+c-a)}}}}
কোসাইন সূত্র
কোসাইন সূত্র (বা কস সূত্র) আসলে পিথাগোরাসের সূত্রের সম্প্রসারিত রূপ। এ সূত্র অনুসারে:
- {\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos C}
বা, {\displaystyle \cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}}
ট্যানজেন্ট সূত্র
- {\displaystyle {\frac {a-b}{a+b}}={\frac {\tan \left[{\tfrac {1}{2}}(A-B)\right]}{\tan \left[{\tfrac {1}{2}}(A+B)\right]}}}
ক্ষেত্রফল
দুটি বাহু a ও b এবং এদের মধ্যবর্তী কোণ C হলে ত্রিভুজের ক্ষেত্রফল কোণের সাইন এবং বাহুদ্বয়ের গুণফলের অর্ধেক।
- {\displaystyle {\mbox{Area}}=\Delta ={\frac {1}{2}}ab\sin C}
হিরনের সূত্রের সাহায্যেও ত্রিভুজের ক্ষেত্রফল নির্ণয় করা যায়। ত্রিভুজের তিন বাহুর দৈর্ঘ্য যথাক্রমে a, b ও c হলে এটির অর্ধ-পরিসীমা,
- {\displaystyle s={\frac {1}{2}}(a+b+c),}
সেক্ষেত্রে ত্রিভুজটির ক্ষেত্রফল:
- {\displaystyle {\mbox{Area}}=\Delta ={\sqrt {s(s-a)(s-b)(s-c)}}={\frac {abc}{4R}}}
যেখানে R হল ত্রিভুজটির পরিবৃত্তের ব্যাসার্ধ।
ত্রিকোণমিতিক অভেদ
পিথাগোরাসীয় অভেদ
নিচের ত্রিকোণমিতিক অভেদগুলো পিথাগোরাসের সূত্রের সাথে সম্পর্কিত এবং যে কোনো মান গ্রহণ করতে পারে।
- {\displaystyle \sin ^{2}A+\cos ^{2}A=1\ }
- {\displaystyle \tan ^{2}A+1=\sec ^{2}A\ }
- {\displaystyle \cot ^{2}A+1=\csc ^{2}A\ }
অয়লারের সূত্র
-
{\displaystyle \sin x={\frac {e^{ix}-e^{-ix}}{2i}},\qquad \cos x={\frac {e^{ix}+e^{-ix}}{2}},\qquad \tan x={\frac {i(e^{-ix}-e^{ix})}{e^{ix}+e^{-ix}}}}
আরও পড়ো-
- সহস্র শর্টকাট পদ্ধতি গাণিতিক সূত্র সহ বাংলায় লেখা বই PDF Free
- ক্যালেন্ডার অঙ্ক শর্টকাট সূত্র
- ঘড়ির কাঁটার মধ্যবর্তী কোণ নির্ণয় করার শর্টকাট পদ্ধতি
- অনুপাত ও সমানুপাত
- কাজ ও সময় সম্পর্কিত অংকের শর্টকাট সূত্র
- ত্রিকোণমিতির অনুপাতগুলো মনে রাখার টেকনিক
- নৌকা ও স্রোত সংক্রান্ত অংক করার শর্টকাট টেকনিক
- লাভ ক্ষতির অংক করার শর্টকাট টেকনিক
ত্রিকোণমিতির সূত্র , ত্রিকোণমিতির সূত্র PDF, ত্রিকোণমিতির সূত্র সমূহ hsc pdf, বিপরীত ত্রিকোণমিতির সূত্র সমূহ, ত্রিকোণমিতির সূত্র সমূহ class 11, ত্রিকোণমিতির সূত্র সমূহ মনে রাখার কৌশল, ত্রিকোণমিতির সূত্র সমূহ class 9, ত্রিকোণমিতিক অনুপাত সূত্র, ত্রিকোণমিতিক অনুপাত সূত্র, বীজগণিতের সূত্র সমূহ pdf, উচ্চতর গণিত ত্রিকোণমিতির সব সূত্র, গণিতের সকল সূত্র সমূহ PDF, জ্যামিতির সূত্র সমূহ,







![{\displaystyle {\frac {a-b}{a+b}}={\frac {\tan \left[{\tfrac {1}{2}}(A-B)\right]}{\tan \left[{\tfrac {1}{2}}(A+B)\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1da4e06eb6f25cd7f7fc1a7784a11a82ae53f9f)










Pingback: ল.সা.গু. এবং গ.সা.গু. অঙ্ক করার সহজ পদ্ধতি PDF | H.C.F. & L.C.M Tricks